Neural network 구조에서 주어진 training 데이터셋에 대해 loss function을 minimize하도록 하는 최적의 parameter 값들을 찾는 과정을 optimization이라고 한다. 이에 대한 가장 기본적인 방법으로서 gradient descent 방식을 공부하였다. Weight parameter들을 initialize하고, 현재 weight 값들에 대해 loss function의 gradient를 구해 그 방향으로 조금씩 이동하기를 반복하면 최적의 위치(weight parameter들이 span하는 공간 상의 위치)를 찾을 수 있다는 것이었다.
포스팅 링크: https://crm06217.tistory.com/18
또한 이 때 모든 training 데이터셋을 매 iteration마다 모두 고려하는 것은 연산이 너무 많기 때문에, mini batch 단위로 몇 개의 데이터셋을 sample 하여 이들에 대해서만 gradient를 구해 weight update를 하는 방법이 보다 실용적이며, 이러한 방법을 SGD(Stochastic Gradient Descent)라고 하였다.
그런데, 이러한 gradient descent 방식에는 한계점들이 존재하는데, 이번 강의에서는 한계점들을 해결하는 advanced optimization 기법들을 공부한다.
Problems with SGD: Jitter & Saddle Points
SGD는 항상 gradient 방향으로 일정한 step 만큼 weight을 이동시키며 update를 하는 방식이다. 그런데, 현재 시점에서의 gradient 방향이 항상 global optimum gradient 방향은 아닐 수 있다. 아래 그림과 같은 경우이다.

이 경우 weight parameter를 벡터로 본다면, 각 dimension마다 gradient의 크기가 다르고, 경사가 가파른 방향으로는 매우 많은 jitter가 생기는 반면, 경사가 완만한 방향으로는 매우 느린 속도로 parameter update가 일어나게 된다.
또 하나의 문제는 global minimum이 아닌 점 중 gradient가 0이 되는 지점에서는 parameter update가 멈추게 된다는 것이다. Local minima과 saddle point에서 이러한 문제가 발생한다. Saddle point의 한글 번역은 안장점인데, 말의 안장의 모양을 떠올리면 된다. 아래 그림과 같은 상황으로, 어느 방향으로는 local minimum이면서 다른 방향으로는 local maximum인 지점이다.
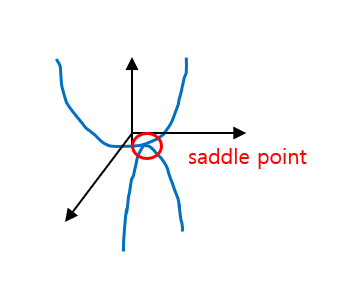
초기값부터 gradient descent 규칙에 의해 이동하다가 이러한 점을 만나면 여기에 갇혀버려서 더 이상 parameter update를 하지 못하고 멈춰버린다.
이러한 jitter 문제와 local minima/saddle point 문제는 weight들의 dimension이 커질수록 더 많이 나타나는 문제이고, 기존의 gradient descent 방식이 갖는 한계점들이다.
SGD with Momentum: Use Previous Gradient Term
Momentum term이 추가된 SGD with momentum의 weight update rule은 아래 수식과 같다.

Momentum term v는 처음에 0으로 초기화되고 이후에는 이전의 v 값과 현재 지점의 gradient를 더한 방향으로 업데이트된다. rho는 friction hyperparameter로서, 만약 0이라면 기존의 SGD와 동일하다. 이렇게 momentum v를 업데이트한 후에, weight은 momentum v 방향으로 업데이트된다.
이를 통해 SGD에서 겪었던 문제점 두 가지를 모두 해결할 수 있는데, momentum term을 통해 이전 gradient 방향에 대한 정보를 누적하면서 weight을 업데이트하므로, local gradient 방향과 global minimum을 향한 방향 간 차이로 인한 high jitter를 어느 정도 완화할 수 있고, local minimum이나 saddle point에서 gradient는 0이더라도 momentum term이 살아남기 때문에 이 지점을 탈출하여 반복을 이어나갈 수 있다.
Variation: Nesterov Momentum
SGD with momentum에 대한 variation으로서 Nesterov momentum 방식이 있다. 마찬가지로 momentum term v 방향으로 weight update가 일어나는데, v에 대한 update rule이 다르다.

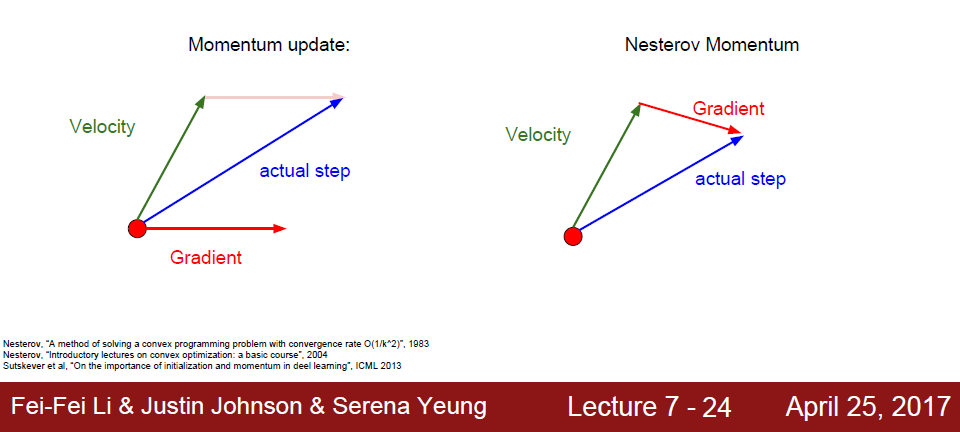
여기서 learning rate alpha와 +, - 부호는 1, 2번째 수식 중 어디에 넣든 상관이 없기 때문에, 결국 다른 점은 v를 업데이트할 때 gradient를 어느 지점에서 계산하느냐이다. 이전 방식은 현재 weight 지점에서 gradient를 계산하고 이 방향으로 v를 업데이트하였는데, nesterov 방식의 경우 weight을 우선 기존 momentum 방향으로 이동시키고 그 지점에서 gradient를 구해 v를 업데이트한다.
강의 자료를 보면 두 방식을 그림으로 비교하였다.
Nesterov 방식을 해석하는 또 다른 방법을 제시하는데, weight W에 대해 W'를 정의한 뒤 W'에 대해 위 수식을 다시 써보는 것이다. 우선 수식은 아래와 같다.
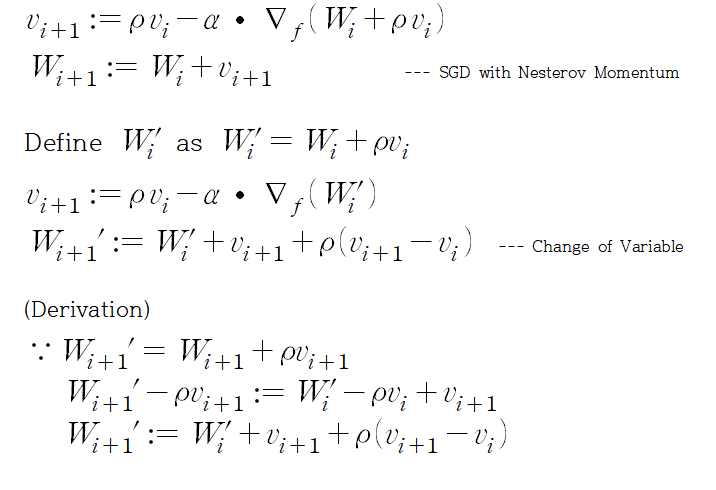
Nesterov 방식에서 weight 지점에서 velocity 방향으로 이동한 지점을 W'으로 정의한다. 그런 뒤, W들을 W'으로 대체하여 수식을 전개하면(derivation 과정), 결과 수식을 얻을 수 있다. 그러면 weight update를 velocity 방향으로 하되, 이전 velocity와의 error correction term을 고려하여 보정한다고 해석할 수 있다.
Global minimum을 찾아가는 과정을 그림으로 확인해보자.
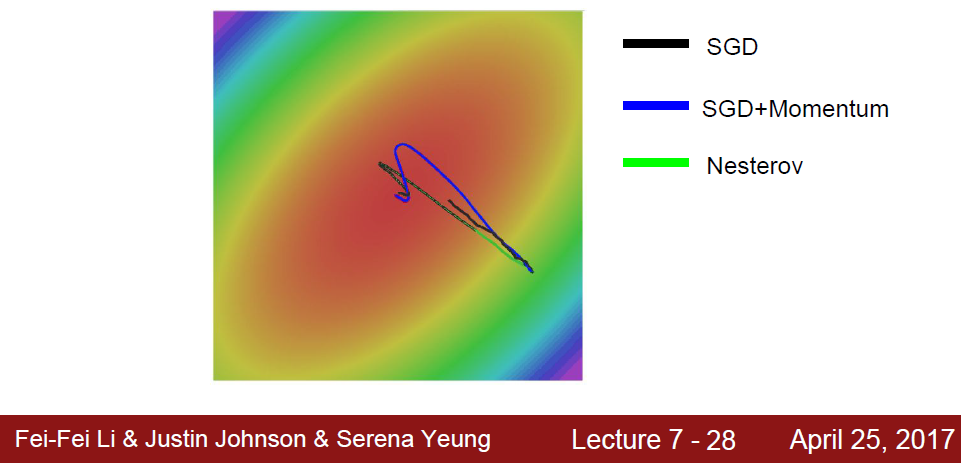
Momentum term을 도입한 경우, overshooting 형태의 경로가 나타나는데, 이는 velocity에 의해 global minimum을 우선 지나쳤다가 error correcting을 하면서 최종적으로 global minimum을 찾아가기 때문이다.
AdaGrad: Use Gradient Squared Term
AdaGrad의 update rule은 다음과 같다.
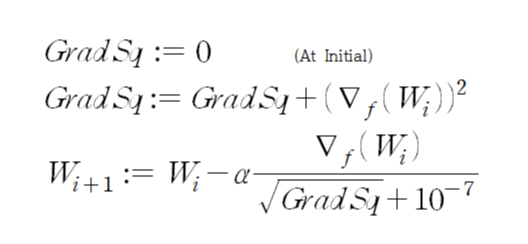
여기서는 velocity/momentum term을 갖는 대신, 초기부터 gradient squared 값을 누적하여 더한다. 여기서 gradient squared란, gradient 벡터를 elementwise 제곱한 것을 말한다. 분모에 10^-7이 있는 것은 초기 상태에서 divide by zero를 방지하기 위한 것으로 보인다.
이 방식은 맨 위에서 SGD가 갖는 jitter 문제를 해결할 수 있는데, 각 dimension마다 누적된 GradSq 값이 다르기 때문에 실제로 update되는 양을 다르게 scaling하게 된다. 만약 경사가 가파른 dimension에 대해서는 GradSq 값이 더 크기 때문에 update 양을 작게 해주게 되고, 그러면 jitter 효과를 완화할 수 있는 것이다.
이전의 momentum 방식과의 주된 차이점이 바로 dimension마다 effective learning rate이 다르다는 것인데, 이에 대해서 'adaptively tune the learning rate'라는 표현을 사용하기도 한다. Momentum 방식은 velocity term을 도입해 또 하나의 방향 벡터를 설정해나가지만, weight을 업데이트할 때는 alpha라는 고정된 learning rate을 사용했다. Adagrad 방식에서는 각 dimension마다 adaptive하게 learning rate을 잡아나간다는 것이 차이점이다.
Adagrad 방식의 한계점으로는 학습의 반복 횟수가 늘어남에 따라 기본적으로 alpha에 곱해지는 term이 작아지기 때문에, effective learning rate이 지속적으로 감소한다는 것이다.
Variation: RMSProp
RMSProp은 Adagrad 방식에서 gradient sqaured를 누적할 때, 그냥 더하는 것이 아니라 이전 accumulated sum을 일정 비율 decaying 시킨 뒤 현재 계산한 gradient squared를 더하는 방식이다. 수식은 아래와 같다.
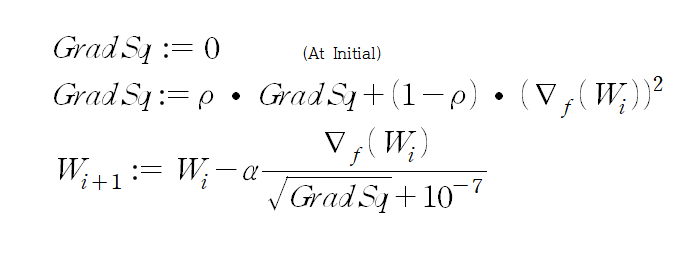
이를 통해 learning rate가 지속적으로 감소하는 것이 문제였던 Adagrad 방식의 한계점을 해결한다.
Adam: Combine Two Approaches
위에서 크게 두 가지 접근법이 있었는데, 첫째는 momentum vector를 추가로 도입하여 이전 gradient 방향에 대한 정보를 바탕으로 update 방향을 보완하는 것, 둘째는 gradient sqaured에 대한 정보를 바탕으로 dimension마다 learning rate을 adaptive하게 설정해나가는 것이었다. Adam 방식은 위 두 가지 접근법을 합친 방식이다. 수식은 아래와 같다.
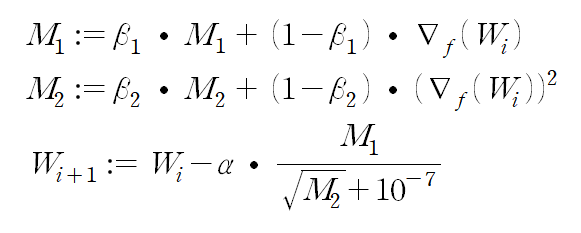
Weight update 수식(마지막 줄)은 RMSProp과 거의 동일한데, gradient 대신 momentum M_1이 사용되었다는 것이 다르다. 강의 자료에서는 momentum term의 초기 조건에 대한 error correction term을 추가하여 다시 개선된 형태까지 제시하는데, 기본 아이디어를 살펴보기에는 여기까지 충분하므로 이 포스팅에서는 다루지 않기로 한다.



