How to Calculate Analytic Gradient for Complex Function?
Optimization 과정에서 loss function의 gradient 방향을 따라서 weight parameter들을 변화시키므로, loss function의 analytic gradient를 계산하는 방법이 필요하다. Lecture 4는 어떻게 복잡한 다변수 함수의 gradient를 계산할 것인지를 다루며, 이를 위해 computational graph와 backpropagation의 개념을 다룬다.
Computational Graph: Forward path & Backpropagation
다변수 함수를 여러 개의 간단한 연산 단위로 쪼개서 node와 연산 gate로 나타낸 것을 computational graph라고 한다. Linear classifier로부터 출발했음을 떠올린다면, computational graph의 맨 왼 쪽에는 input image의 픽셀 값과 weight 값이 있을 것이고 맨 오른쪽에는 loss function L이 있을 것이다. 여기서는 개념을 소개하는 단계이므로, 이러한 복잡한 함수보다 간단한 함수를 먼저 다룬다.
강의 노트에 소개된 간단한 예제를 살펴보도록 한다.

input으로부터 함수의 값을 차례로 계산해나가는 것을 forward path라고 한다. 연산 gate의 input 노드의 값들을 대상으로 특정한 연산을 수행한 뒤 결과가 output 노드의 값이 되는 과정을 반복하는 것이다.
다음으로 backpropagation은 이름에서 알 수 있듯이 역방향으로 일어나는 연산인데, 기본적으로 chain rule을 이용해서 역방향으로 local 변수에 대한 전체 function의 gradient를 계산한다는 아이디어이다.
아래 그림에서 하나의 연산 gate에서 어떤 일이 일어나는지를 표현하였다.

우선 파란색 화살표는 forward path로서, 연산 gate가 명시하는 연산 f에 따라 input x, y로부터 output z의 계산이 이루어진다. 여기서 아래첨자로 0이 붙은 것은 실제 값을 나타낸다.
다음으로 빨간색 화살표는 backpropgation으로서, 우선 맨 오른쪽을 보면 loss function의 z에 대한 gradient가 오른쪽에서 propagate되었다. 만약 여기가 맨 마지막이라면 trivial case로 자기 자신에 대한 미분이므로 바로 1로 계산될 수 있다. 그리고, 이 값과 local gradient를 곱함으로써 연산 gate의 두 input 노드인 x, y에 대한 gradient를 계산한다. 여기서 local gradient는 연산 gate에 의해 정의되는 것으로, 오른쪽으로부터 전파되어 온 gradient와 연산 gate의 local gradient가 곱해져서 왼쪽으로 계속 전파된다.
Simple Gate Examples
addition, multiplication, max gate를 거치는 backpropagation에 대해 조금 더 직관적으로 이해를 해보자.
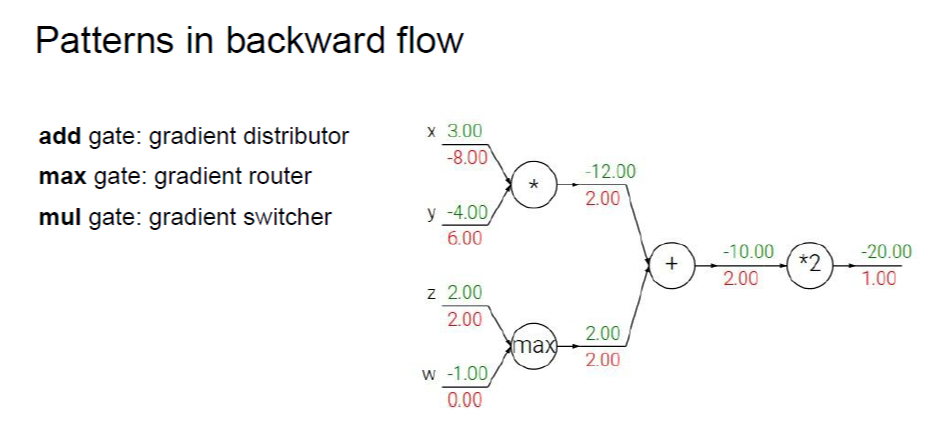
1) addition의 경우, z=x+y와 같이 표현되므로 두 input 노드에 곱해지는 local gradient는 둘 다 1이다. 즉, 오른쪽에서 전파되어온 gradient를 그대로 분배하는 효과를 준다.
2) max의 경우, 더 큰 input 노드 쪽으로는 오른쪽에서 전파되어온 gradient를 그대로 넘겨주고, 작은 쪽은 0을 곱한다. 이러한 맥락에서 routing 하는 효과를 준다.
3) mult.의 경우, z=x*y와 같이 표현되므로 각 input 노드에 서로 다른 input 노드 값을 local gradient로서 곱해준다. 이러한 의미에서 switcher라고 표현하였다.
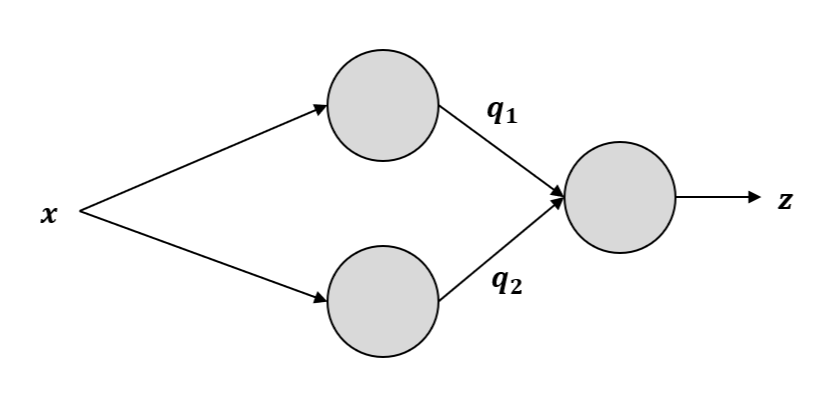
4) branch: 위의 그림과 같이 하나의 노드가 여러 개의 gate의 input으로 갈라지는 경우인데, 이 때는 (오른쪽 방향에서) 연결된 gate들로부터 전파되어온 gradient를 모두 더해준다. 더하는 이유는 multivariable chain rule로부터 그러하며, 수식은 아래와 같다.
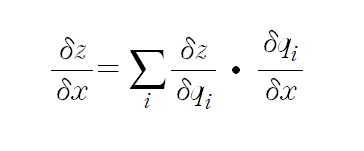
More Complex Gate: Sigmoid
addition, multiplication과 같은 매우 기본적인 단위로 다 쪼개서 노드와 gate를 표현할 수 있지만, 때로는 더 큰 단위로 묶어서 나타내는 것이 유용한 경우도 있다. 예를 들어, 앞으로 쓰이게 될 sigmoid 함수에 대한 연산 gate를 살펴보자. 연산 gate에서 중요한 것은 forward path의 수식, 즉 연산 gate가 명시하는 연산과 input에 대한 local gradient 수식이다.
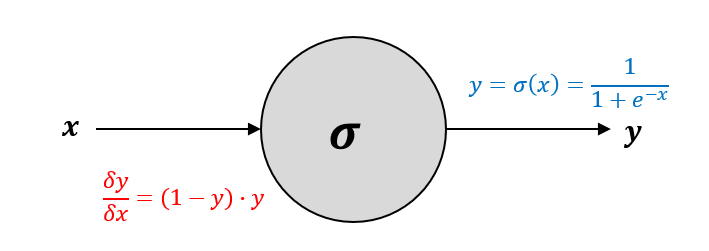
sigmoid gate의 local gradient 유도 과정은 다음과 같다.

Expand to Vectorized Operation
위에서는 연산 gate의 두 input이 스칼라, output도 스칼라인 경우를 살펴보았다. 이제 이를 벡터 연산으로 확장해서 생각해보기로 한다.
우선, 다변수 벡터장에 대한 미분으로서 야코비안 행렬(Jacobian Matrix)이라는 개념이 존재한다. 여기서는 공학의 관점이므로 input, output이라는 표현을 사용하면, input이 n-dim, output이 m-dim 이라면 야코비안 행렬은 (m, n) 차원의 행렬이 된다. 그런데, neural network의 맥락에서는 벡터 연산이라고 해서 꼭 야코비안 행렬 전체를 구할 필요는 없다. 야코비안 행렬의 크기가 input, output 차원의 곱으로 커지는 것도 문제이지만, 자주 사용되는 벡터 연산의 경우 elementwise 살펴보았을 때 보다 단순한 꼴로 표현 가능하기 때문이다.
Vectorized max Operation
예를 들어, (n, 1) 벡터에 대해 0과의 max 연산을 하는 gate를 생각해보자. 이 경우, input element 하나가 정확히 output element에 대응되도록 연산이 이루어지므로, 야코비안 행렬을 구하더라도 diagonal entry만 존재할 것이다. 따라서, 야코비안 행렬을 구하기보다 elementwise 살펴보면, 위에서 다루었던 스칼라 max gate를 n개 가져다놓은 것과 같은 상황임을 알 수 있다. 따라서 위에서 했던 gradient router의 개념을 적용 가능하다.
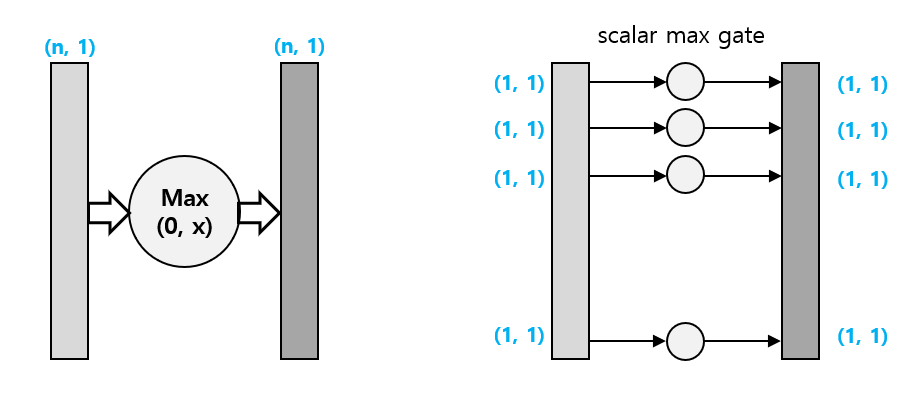
Another Example: Vector Multiplication & L2 Norm
이번에는 벡터 곱셈이 들어간 연산 gate 예시를 살펴보자.

이를 중간 노드 q를 사용해 두 개의 gate로 표현하면 아래 그림과 같다.
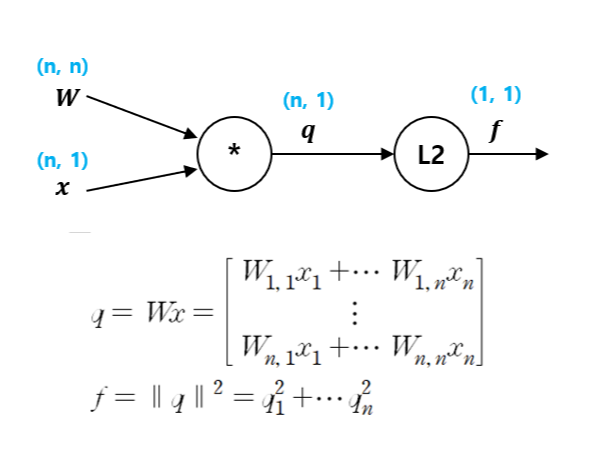
먼저, L2 gate의 local gradient를 구하기 위해 벡터 q의 i번째 element에 대해서 계산한 뒤 이를 벡터의 형태로 표현한다. f가 q에 대해 표현된 수식으로부터,

Gradient를 구할 때 항상 생각해야 할 것은 gradient 결과의 차원은 gradient를 구하는 변수의 차원과 일치해야 한다.
다음으로 q의 gradient를 W, x에 대해 각각 구하면 이 gate에 대한 local gradient들을 모두 구하게 된다.
W에 대해 gradient를 구하는 과정은 다음과 같다.

마찬가지로 elementwise gradient를 먼저 구한다. 벡터 q의 k번째 element에서 행렬 W의 (i, j) element의 영향을 보는 것이다. 위 수식으로부터 만약 k와 i가 다르다면 W의 (i, j) element 자체가 존재하지 않으므로, indicator function을 사용하여 나타낸다. k와 i가 같은 경우에 한하여 이를 W의 (i, j) element로 미분하면 x_j가 나온다.
이제 multivariable chain rule에 의해 f의 gradient를 W의 (i, j) element에 대해 계산하면 sigma와 indicator 함수가 합쳐지면서 k 변수가 없어지면서 수식이 정리된다. 그리고 마지막에 elementwise 결과로부터 vectorized form으로 바꾸어 쓰는 부분이 있는데, 이는 elementwise 수식에 대한 관찰로부터 이루어지며 따로 공식이 있는 것은 아니다. 이 경우 두 벡터의 곱의 형태를 띤다는 사실로부터 위와 같이 정리할 수 있었다.

x에 대한 gradient도 마찬가지로 구할 수 있다. 벡터 q의 k번째 element에는 항상 x의 i번째 element가 존재하고, 이것으로 미분한 것은 x 앞에 붙은 계수인 W의 (k, i) element이다. 여기서도 마지막에 elementwise 수식 결과를 vectorized form으로 바꾸었는데, x의 i번째 element를 계산하는 데에 쓰인 W, q의 element들을 확인해보면 아래와 같다.
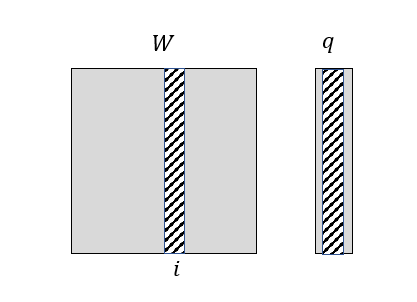
이를 통해 W를 transpose 시킨 뒤 q와 곱하면 위 elementwise 수식과 일치할 것임을 알 수 있다.
More on Matrix-Vector Multiplication...
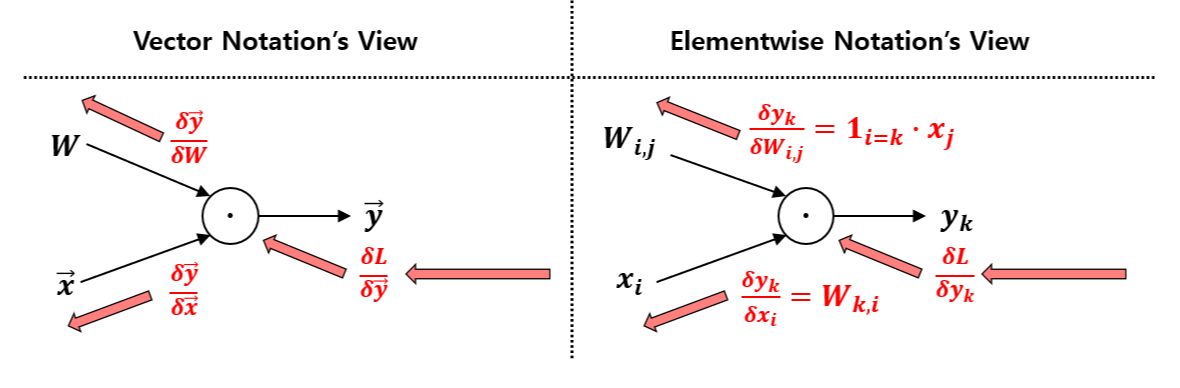
스칼라 연산 gate가 깔끔하게 정리되었던 것과 달리 vectorized 연산 gate는 처음 보기에 덜 깔끔한 부분이 있다고 느꼈는데, 마지막에 elementwise gradient를 구한 것을 vector 형태로 변환하는 것이었다. 왜냐하면 input, output 차원에 따라 경우의 수가 다양하게 존재하는데, 이에 대한 변환은 상황에 따라 알아내야 하는 것처럼 보였기 때문이다.
여기서 우선 결론을 낸 것은, local gradient의 vector 형태로의 변환이 필수적이지는 않다는 것이다. gradient가 실제로 쓰이는 gradient descent에서 parameter 업데이트하는 부분을 생각해보면, 결국 실제 연산은 elementwise로 이루어진다. 그렇기 때문에 vector notation으로 깔끔하게 표현이 되더라도, 실제 컴퓨터에서 각 gate마다 backpropagation을 수행할 때는 elementwise 계산될 것이다. 따라서, local gradient의 수식은 elementwise로 정리하면 충분하다는 결론을 얻을 수 있다.
'Deep Learning > cs231n Lecture' 카테고리의 다른 글
| Lec 5. Convolutional Neural Network, Convolution Layer, Max Pooling Layer (0) | 2023.03.16 |
|---|---|
| Lec 4-2. Introduction to Neural Network (0) | 2023.03.13 |
| Lec 3-2. Optimization: Gradient Descent, Stochastic Gradient Descent (0) | 2023.03.06 |
| Lec 3-1. Loss Function: Multiclass SVM, Softmax, Full Loss (0) | 2023.03.02 |
| Lec 2-2. Linear Classifier: Parametric Approach, Interpretation, Limitation (0) | 2023.02.27 |



